Magnetic levitation devices are mainly divided into two kinds: power drive, and powerless drive.

Powerless levitation is divided into two categories: superconducting levitation and ordinary magnetic levitation. The former is achieved by the complete anti-magnetism of the superconductor, which is installed between the superconductor and the magnet as if it were a spring. Simply put, any movement of the magnet near the superconductor generates a current on the surface of the superconductor, and the magnetic field generated by this induced current impedes the movement of the magnet, so the magnet becomes relatively stationary with the superconductor. Ordinary magnetic levitation can be divided into two categories, repulsive levitation, and attractive levitation. Repulsion levitation has a finished product available for purchase, the so-called gyroscopic levitation. The principle is to use five large magnets (such as the four corners of four N-pole up, the middle piece of S-pole up) in the levitation space above the generation of a magnetic field valley (N-pole down the levitation magnet around the repulsive force is strong but weak in the middle), then as long as the polarity of the levitated magnet is maintained, you can successfully levitate. But in the free state of the magnet will be reversed up and down, and the repulsive force into an attractive force, the result of levitation will fail. The solution to this problem is to make the levitating magnet into a gyroscope to ensure that the polarity is not reversed during operation so that it can levitate. This “toy” I bought a long time ago, levitation requires skills, the weight of the gyroscope to be adjusted by shims to within 0.1g error in order to levitate, and requires a very flat base.
The above levitation either requires energy or conditions that will not last (low temperature of superconductivity, gyroscopic rotation), so none of them is a permanent levitation solution.
The last one is attraction levitation. However, in attraction levitation, the attraction of two magnets is basically inversely proportional to the square of the distance, although the suction force has an equilibrium point with gravity, but for non-stable equilibrium.
- Powerless adsorption of the rejection of levitation
Magnetic levitation gyro is a good thing, the major e-commerce platform can be bought, good value for money. After some relentless attempts, there are many people who can see with their own eyes a rotating gyro floating in the air, however, why the levitating gyro can float in the air is indeed unexplained.
Viewpoint 1: Two magnets attract each other, and the same sex repels each other, so they can naturally be levitated. This is obviously not true. Otherwise, why do we bother to rotate it?
Point 2: It can’t float stably in the air if it doesn’t rotate. But just as a spinning gyroscope will not fall, a spinning magnetic gyroscope will be able to float steadily over a large magnet. Physicists say that this property of a gyroscope that does not fall down is due to the conservation of angular momentum.
This statement seems to make some sense. But let’s examine why it is not true either.
To understand the error in the second statement, we must also start with the error in the first statement. There is a magical law (Earnshaw’s law) that proves that any combination of electrostatic force, static magnetic force, and gravitational force (the gravitational force described by Newton’s law) cannot put an object in stable equilibrium.
What is a stable equilibrium state? A small ball at the bottom of the bowl is in a state of stable equilibrium, that is, no matter which direction you gently push it, it can return to the bottom of the bowl, physicists say, this is because the gravitational potential energy of the ball in the bottom of the bowl has a minimum value. Objects like to stay in the lowest potential energy place, as the saying goes, water flows downhill.
There is a stable equilibrium then there is an unstable equilibrium. What is unstable equilibrium? Putting a small ball on top of a large ball is an example. In this case, if you slightly on the small ball and blow a breath it will slip down, and can not come back. Physicists say that this is because the gravitational potential energy of the small ball on top of the ball is the maximum, it stays there restless. In addition to these two cases, there is a more special state. If we put a small ball in the center of the top of this saddle-shaped gymnasium below, what will happen? The situation is that if we push the left and right direction of the ball it can still return to the center, before and after pushing it can not return. Physicists say that the gravitational potential energy of the ball has a “saddle point”, that is, it is a stable equilibrium in one direction, and the other direction is an unstable equilibrium. More than one hundred and sixty years ago, Mr. Ensor proved that all electrostatic fields, static magnetic fields, and gravitational fields on a charged body or a magnet-generated potential energy are saddle-shaped. That is, by these three forces, a small magnet cannot be suspended in the air; it will always slip away in one direction or another.

A complete and correct explanation of the stability problem of hovering gyroscopes was first given around 1996 by the famous British theoretical physicist Michael Berry, a remarkable physicist, who proved that a spinning gyroscope, by some miraculous action, changes what was a saddle-shaped potential into a bowl-shaped potential. How did this happen? It turns out that Ensor’s law proves the case that if you can keep a small magnet always facing in one direction, then the magnetic field potential it is subjected to is saddle-shaped. We all have this experience of holding a small magnet at the end of our fingers, same-sex near another large magnet fixed on a table, and we feel the small magnet is eager to slip to one side. Here, this three-dimensional saddle situation can be stable in the vertical direction, while the horizontal direction is unstable. However, the gyroscope can turn the horizontal direction into a stable as well when it is rotating. This is because the angular momentum of the small magnet, the magnetic field, and the magnetic field of the large magnet interact so that when the small magnet tries to move horizontally to the right, its axis of rotation no longer remains upright but follows the local magnetic line of force tilted slightly to the right. Likewise, when it tries to move horizontally to the left, its axis follows the local magnetic line of force and tilts slightly to the left. Amazingly, this is exactly the opposite of viewpoint two. The second view is that the gyroscope, due to the conservation of angular momentum, is always upright and even steadily levitates; in reality, the small gyroscope is able to intelligently follow the direction of the local magnetic line of force to adjust the direction of its own axis of rotation and make itself steadily levitate. This should be a reflection of keeping up with the times!
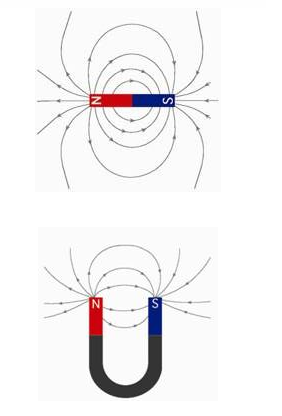
Because the gyroscope is not always pointing in the same direction, Ensor’s law no longer applies. In this case, the potential energy felt by the levitating gyro magnet is indeed a bowl rather than a saddle, and although it is a very shallow and shallow bowl, the gyro is stable and balanced at the bottom of this bowl, enough to resist air disturbances, and you can’t easily blow it away by blowing on it. Physicists call this bowl a potential well, very graphic, right?
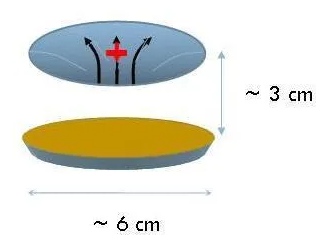
Mr. Berry’s calculations show that this bowl-shaped potential well occurs in a very small area above a magnet (if the magnet base is 6 cm in diameter, this equilibrium interval is between 3 and 3.8 cm), so the weight of the hover gyro must be adjusted just right to hover in this interval. Too light or too heavy, the hover gyro can not be balanced in this zone.
The principle of static magnetic levitation is being applied in costly scientific experiments. For example, the magnetically confined neutron experiment. Because neutrons are not charged, they cannot be controlled by electric fields. But neutrons have a spin and a magnetic field, is it not the equivalent of a small levitating gyroscope?

